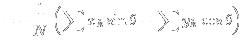平面上の点を近似する直線
プログラムを作っていて、平面上に散らばった点を直線に近づけるように力をかけたいという問題にぶちあたった。
しかし、Google で探してもみつからない (笑) ので、自分で解く羽目になった。せっかくなのでwebに貼っておけば、 誰かが参考にするのではないかと期待してはってみる。間違いがあったら連絡ください。
方向ベクトル
![]() の直線
の直線 ![]() の方程式は
の方程式は
点
| (2) |
直線
| (3) |
| (4) | ||
| (5) |
式 (5) は
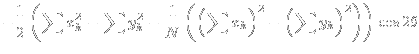 |
||
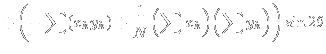 |
||
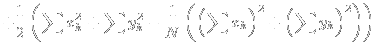 |
(7) |
ここで
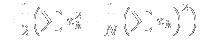 |
(8) | |
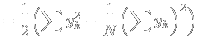 |
(9) | |
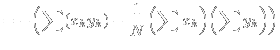 |
(10) |
とおくと
| (11) | ||
| (12) | ||
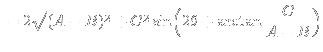 |
(13) |
 |
(14) |
このとき
| (15) |
![[Makino's Page]](/~t/img/xBannerLeft24.png.pagespeed.ic.yx6lsWjDp1.png)
![[Between Man and the Moon]](/~t/img/xBannerRight.png.pagespeed.ic.DOFE24z6u6.png)